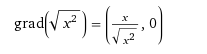Numerical Instability in `tf.norm`

TL;DR there’s a bug in tf.norm that’s been open since 2017 and you should be careful when using it.

Consider the following snippet:

x = tf.constant(0.1)
with tf.GradientTape() as tape:
  tape.watch(x)
  y = tf.norm(x * x)
grad = tape.gradient(y, x)  # Returns correct gradient, 0.2

However if x is 0 or close to 0, the gradient is incorrect (NaN).

x = tf.constant(1e-30)  #  
with tf.GradientTape() as tape:
  tape.watch(x)
  y = tf.norm(x * x)
grad = tape.gradient(y, x)  # Returns NaN

This code is the culprit.

It’s simple math: let’s say you want the L2 norm.

sqrt((x1-x2)^2 + (y1-y2)^2 + … )

If you have a single variable (simplest case) it boils down to

sqrt((x1-x2)^2) or just sqrt(x^2)

The gradient of this when x is small is undefined.