Overfitting

This far in my (short) professional career I’ve built / used simple models (mostly SVMs), counting methods, time-series analysis, and graph processing / clustering in the service of fighting spam and abuse. Contrary to what people might assume, even companies with significant ML talent such as Facebook and Google have only just begun applying complex models to tasks such as abuse fighting. In a world where false positives on customers cost a lot of real money and goodwill (…which also translates to money), it’s important to get things right and fix them when things go wrong. This is very tricky.

There are major caveats to using ML tech that is not easily understandable. So with the growing prominence of “deep learning applied to everything” it’s important to know when a complex model fits your problem.

The High Interest Credit Card of ML

That subtitle is the title of a very good paper from Google that is definitely worth checking out.

Part of the deep learning hype is the unreasonable efficacy of neural nets: given a large amount of data encoding unknown features, automated feature selection often yields measuably better results (on test sets) than hand-crafted features + an equivalent ML model. Previously wisdom was that more data is more important than complex classifiers, but with deep nets the practical effectiveness gains on tasks such as ASR and image recognition are taking previously unusable technologies to new levels of awesome (e.g Siri, Cortana, Amazon Echo, Toytalk).

So why not use deepnets for everything? One answer is that the previous wisdom wasn’t all wrong: complex classifiers that learn more nuanced functions also require huge samples of the search space they’re trying to learn. Another aspect (and the one we’ll talk more about here) is that it’s difficult to intuit how things can go wrong. When things do go wrong you will likely be responsible for debugging the model you built.

Julie Evans has a really great checklist that can help make good ML decisions. From the post:

A model you don’t understand is

• awesome. It can perform really well, and you can save time at first by ignoring the details.
• scary. It will make unpredictable and sometimes embarrassing mistakes. You’re responsible for them.
• only as good as your data. Often when I train a new model I think at some point “NO PLZ DON’T USE THAT DATA TO MAKE DECISION OH NOOOOO”

Some way to make it less scary:

• have a human double check the scariest choices
• use complicated models when it’s okay to make unpredictable mistakes, simple models when it’s less okay
• use ML for research, learn why it’s doing better, incorporate your findings into a less complex system

At a previous company we often used linear SVMs + hand-engineered features to detect spam and abuse. The reasoning: it is too expensive to have false positives, and it isn’t OK to make unpredictable mistakes. If you do make a mistake, you have to be able to explain it.

But what does it mean to be able to explain your mistakes, and where do we draw the line between complex and simple models?

Overfitting the World

Using “understandable models” as a concept may seem vague and arbitrary but there is rigor in sight. Specifically, there is a more rigorous answer to the question: “why not use RBF Kernels in my SVM? It seems like we get better results on our test set when we increase the ‘complexity’ of our model.”

The answer lies within VC Theory. (The basics of Vapnik-Chervonenkis theory are less intimidating than their names make it sound.)

Imagine you have 3 points being classified positive or negative. A question you can ask is, “is it possible to draw a line that separates the three points perfectly into positive and negative halves?” Let’s try:

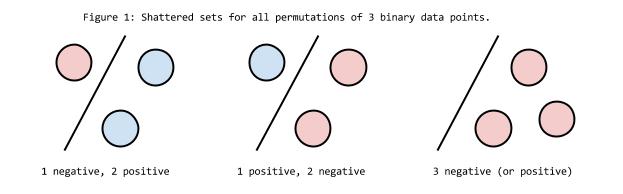
As you can see, 3 points can always be separated into positive and negative groups perfectly (provided they are not in a line). However, if you have 4 points, it becomes impossible to separate them with only a single line.

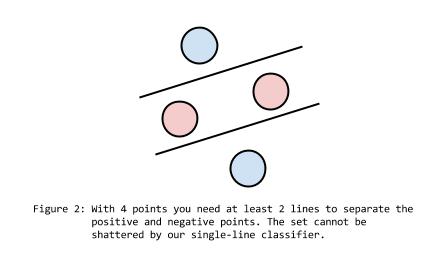
Since 3 is the limit for # of points perfectly classified by a single line, a classifier that draws a single line can be said to have a VC dimension of 3.

Now of course most classifiers draw something more complicated than a single line (e.g polynomial SVMs draw a family of functions in N-dimensional space). But the principle is the same – given n (binary) data points you have 2^n possible labelings. And if your classifier can separate the points perfectly, that set is considered shattered. VC dimension is an upper bound on the separating power of your classifier.

Note that a function family with VC dimension n is not guaranteed to shatter all possible sets of n points, it only is guaranteed to shatter some set of n points. This is why we call it an upper bound: if your VC dimension is 5, you’re guaranteed that no set of 6 points can be shattered by your classifier.

Knowing the VC dimension for a given classifier is really good: it lets you predict an upper bound on the test error of your classification model. In other words, you can know rather definitively whether your model overfits the test set. And I think that lets us define a rigorous / discrete criteria for “understandable model” – if you know you can’t overfit, you can understand (in a very specific sense of that word) the model.

The details are more complicated, but can you guess why RBF kernels aren’t good when you need understandability? That’s right: you can’t bound their VC dimension. And deep neural nets are the same. That means they have effectively infinite separating power, and can always overfit your data. This isn’t true for linear and polynomial SVMs, which have bounded VC dimension.

So now we have some rigor: when people talk about complex models, they’re referring to any model that is non-convex (we can’t figure out the VC dimension). When they talk about understandability, a big part of that is answering the question “did my model overfit.”

Practical Matters

“So, are you telling me that you can’t know if my complex model overfits?”

Yes, There’s no theoretical assurance that a given complex model will work in practice. There is no shattered set proof for neural nets. However, from a practical perspective cross-validation does a good job of telling us whether our models work. Cross-validation (or if you have enough data, holdout validation) depends on your collected data being representative enough of the population and means nothing if it contains a lot of skew.

So if you work for a small company or something and can’t hope to collect a dense enough sample of points to have any sort of confidence interval for how similar your collected data is to the population, you should probably err on the side of a simpler model.

And when you inevitably reach for that small model, you still have to do a bunch of gut-checking.

Julie Evans says in her blog post: “a model you don’t understand is only as good as your data.” Whatever biases exist in your data will exist in your bleeding-edge-definitely-overfitting-mega-complex-model. These biases can be pretty awful.

Which Classifier?

Since there’s no upper bound for the separating power of RBF SVMs and Neural Networks, we consider them complex models at risk of overfitting. However the same is true of bounded models: a classifier with very high VC dimension is at higher risk of overfitting than one with lower VC dimension, since VC dimension gives an upper bound on separating “power.”

A rule of thumb is to choose the lowest-power classifier you can get away with and still have decent accuracy. However if all your accuracy is coming from overfitting… you may still end up with problems (something every deep learning enthusiast has to contend with).

If you do choose a high-power classifier, you need to pair it with a dense sample of the space you want to classify. You also need to be ready to apply some more advanced overfitting protections (regularizers).

What you find in the more common case is smaller amts of data, less clean data, and high cost error penalties. In these cases other approaches work well. Some interesting bits I learned via practical applications:

• Linear and simple polynomial SVMs work really well for basic spam and abuse fighting. I’ve seen that RBF kernels can be really good too given enough data and very careful approach. The theory behind SVMs is still more complete than neural nets as of now; a lot of the parameter tuning for neural nets is actually guessing / not based on any rigorous theory.

• Random Forests work incredibly well for many datasets for a few reasons:

  • You don’t need to normalize your data. If you have something scaled from 0-1, and some other signals scaled from 0-10000, it’ll still work since it just needs to choose a splitting point.

  • Many datasets are medium-small, and mediocrely labled. This makes many of the more complex models weaker, but also SVMs. In practical cases like these Random Forests seem to get the job done better.

  • Random forests are very easy to visualize. You can in many cases turn your classifier into procedural code (a series of if statements over feature vectors) that can be manually inspected!